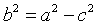The Hyperbola

Ready to take a look at the third conic section? (The first two we looked at were the parabola and the ellipse). The hyperbola is created when the plane passes through both nappes of the right circular conical surface at an angle with the surface’s longitudinal axis that is less than the angle made with the axis by the generating straight line on the surface.

The hyperbola is found in many natural phenomena including an open orbit of celestial bodies or simply the curvature of light around a large gravitational body like a star. It is also the path of subatomic particles repulsed by the nucleus. In more everyday terms, the tip of a shadow cast by the sun traces out a hyperbola on the ground as the day progresses. The mathematics of hyperbolas is also used in navigation and global positioning systems.

The definition of a hyperbola that we will use to develop an algebraic expression is similar to that of the ellipse. A hyperbola is all the points in a plane the difference of whose distances from the two foci is a (positive) constant. The ellipse was simply the sum instead of the difference.

We begin with the hyperbola centered on the origin in a Cartesian-coordinate plane. As with the ellipse we use the foci, (c,0) and (-c,0). The distance from each focus to a general point (x,y) is given by the following two expressions using the two-dimensional distance formula:

Now using the above definition we will set the difference between these two to a constant number, 2a, just as we did with the ellipse. One important thing to note is since as we move about the plane the difference between these may change from negative to positive or positive to negative depending on which distance is longer. We will use the absolute value to insure we get the magnitude of the difference in distance.

As with the ellipse, using some elementary algebra we arrive at:

Now “a” represents the x-intercepts or the vertices. (Let y=0 and multiply both sides by “a” squared). With the ellipse, “a” was always greater than “c” so we factored out a negative 1 from the denominator of the second term and changed the sign between the two terms to a positive. Then we used the substitution:

In the present case, “a” will always be less than “c” so we use the substitution:

This yields the final expression:

Notice here that if we try to locate the y-intercepts by setting x=0, we get imaginary results. (Square root of negative “b” squared). Therefore this is the expression for the hyperbola with vertices on the x-axis. The expression for the hyperbola with vertices on the y-axis is:

Just as with the parabola we can use the same substitutions for translation and axes and rotation of axes to develop expressions for more general hyperbolas.

The axis that runs through the vertices is called the transverse axis. The axis that is orthogonal to the transverse axis is the conjugate axis. A hyperbola is often drawn by constructing a rectangle that is 2a by 2b in dimension with the vertices on the 2a length sides. Then diagonals are drawn through the rectangle and used as asymptotes for the hyperbolic curve. The equation for these asymptotes can be derived by solving the main equations for y.